「ゼロから作る Deep Learning」で機械学習を学ぶ その03 誤差逆伝播法の導入
2025-07-23 12:56:44
- Tags:
- Python
- Deep Learning
今回は第5章「誤差逆伝播法」
ソースは下記
ryotakato/de_zero
前回で学習は作ったが、
1世代学習するのに僕のマシンだと10秒ぐらいかかってしまい、かなり遅かった。
そこで、この章の誤差逆伝播法の出番である。
今までの偏微分の勾配を求める方法だと、1パラメータ(これは重みやバイアス1つ1つという意味)毎に損失関数を計算しなくてはいけないので、
パラメータや層が多くなればなるほど、それが2乗のオーダーで計算時間が増えていた(正確には、毎回偏微分で2回関数を実行しているから、2乗の2倍)
そこで、今回は偏微分を解析的に考え、最終的な数値の違いを変えることで、元の値がどの程度変化するのかを考えることで、
毎回関数を実行しなくても、簡単な演算(四則演算や行列計算)のみで損失関数を計算できるというもの。
結構実装は簡単だし、書籍で説明されているものはよく理解できるんだけど、
これ自分で思いついてプログラムを書こうと思ったら、微分解析学をちゃんと理解していないといけない。
あー、大学生のころちゃんとやっておけば良かった。。。
もう忘れたわ。
とりあえず実行結果。
10000回実行して、
損失が減っていく様子、計算精度がtrainデータとtestデータでどちらも高くなっていくのが分かる。
なお、epochは今回は600回なので、10000回で16epochほど。
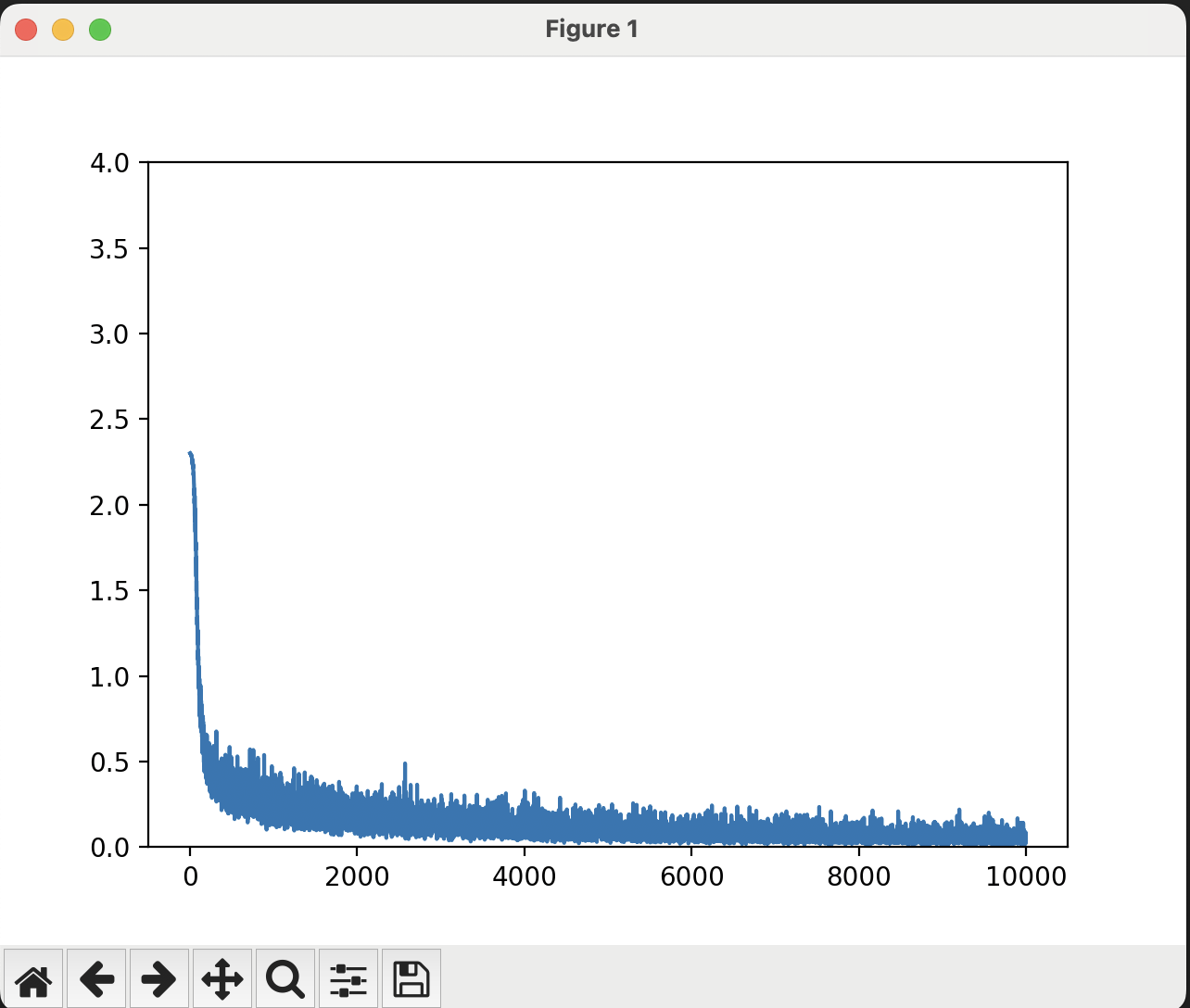
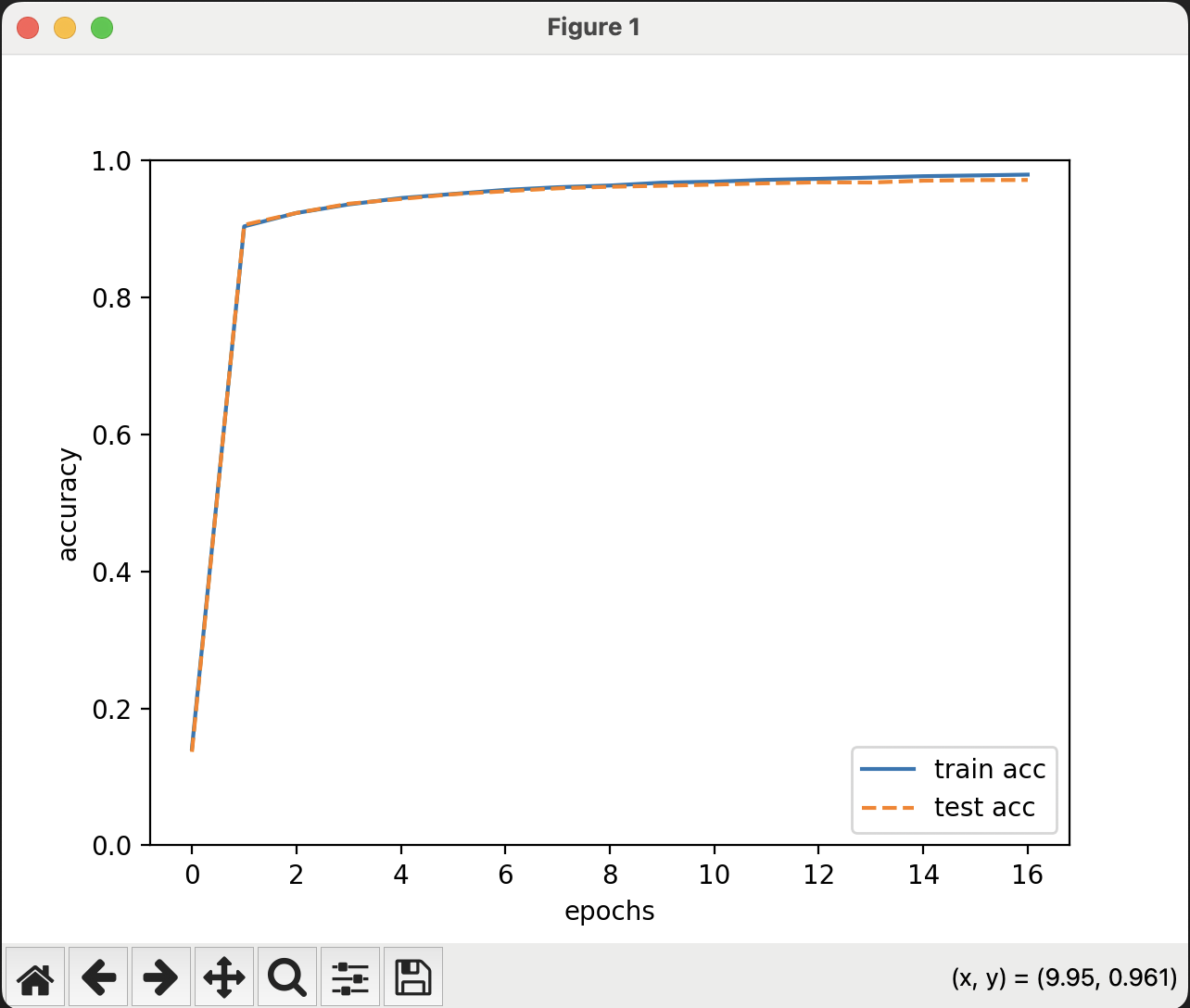
実行する前は、まあ1000回で3時間ぐらいかかっていたのを、
10000回で1時間ぐらいで終わるならいいかなって思っていたんだけど、
なんと実行してみると、10秒以内に10000回終わってしまった。
まじかよ、めっちゃはえーじゃん。。。
ナニコレ、誤差逆伝播法すげー。
方法を変えることで、速度が比較にならないぐらい変わるっていうの、
仕事でソフトウェア開発やっているときも何度もあるもんね。
ということで、次は第6章で、
ここからは精度をもっと高めていくための方法みたい。
なんだけど、ちょっと都合で新しいMacを買ったので、そっちのセットアップに時間を取られるかもしれない。
M4なので、上記の計算がもっと早くなるかもね。


There are currently no comments on this article, be the first to add one below
Add a Comment
Note that I may remove comments for any reason, so try to be civil. If you are looking for a response to your comment, either leave your email address or check back on this page periodically.